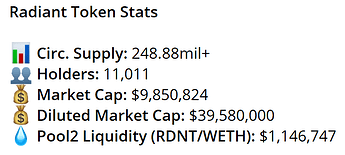
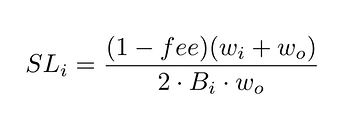For reference, $RDNT token stats (12.20.22):
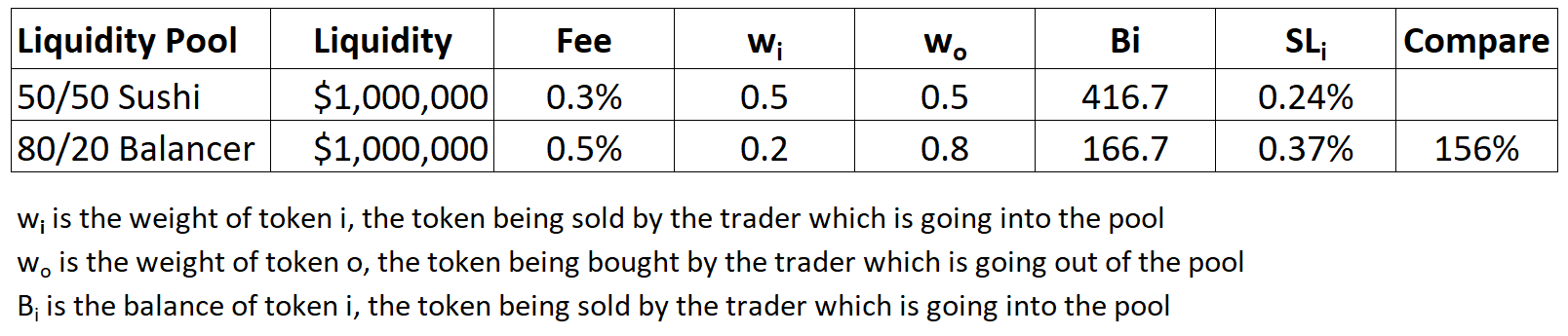
For simplicity, let’s assume a baseline liquidity of $1M and an ETH price of $1,200. I’ll also use ETH instead of changing to wstETH.
Linearized slippage formula:
Using this formula, slippage would increase from 0.24% to 0.37% for a 1 ETH swap for $RDNT, a 56% increase if the LP size remained the same. But now, there will be no incentives to locking $RDNT, so a portion of locked $RDNT will move to this new LP.
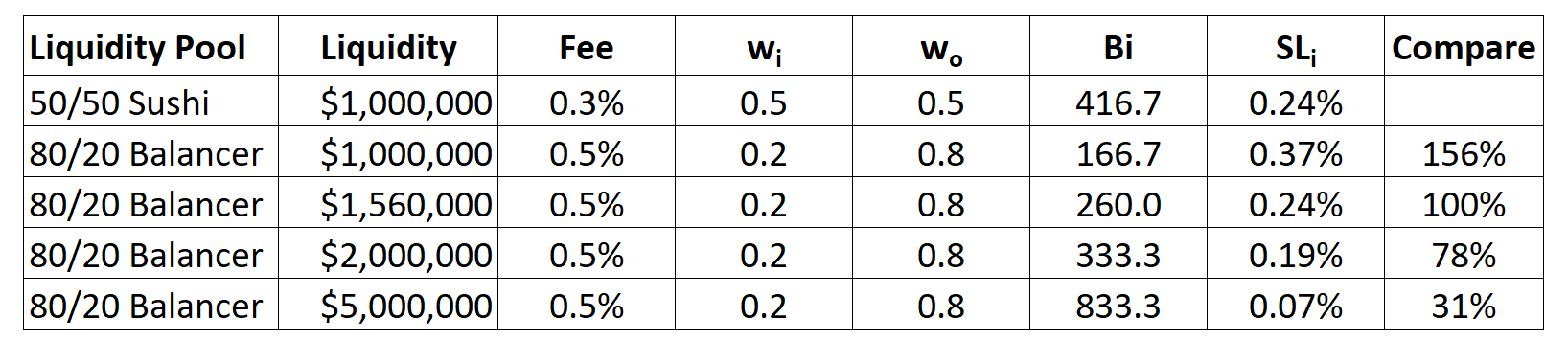
In order to break-even on slippage, $560k additional liquidity would need to be added. This is 5-6% of the $RDNT market cap and with incentivization to move those tokens into an LP, this seems very feasible.
Let’s say the LP doubles, slippage would then decrease to 0.19% or 78% of baseline for a 1 ETH swap. Lastly, let’s say the LP reaches $5M (~half $RDNT market cap), slippage would decrease to 0.07% or 31% of our baseline scenario.
With the heavy incentivization of the LP and much lower impermanent loss, the additional capital attracted will more than offset the price impact changes and on a net basis, will improve liquidity and reduce slippage overall on-chain.
Some additional items to consider:
- Using a liquid staking derivative on Balancer would be eligible for one of Balancer’s core pools, with 50% of protocol fees refunded to the LP pool.
- LPs also get to take advantage of staked ETH yield on top of the fees earned as an LP.